STATISTICAL PROCESS CONTROLL
Cominciamo col definire un Controllo Statistico di Processo (SPC Statistical Process Controll). Universalmente riconosciuto (e utilizzato anche per la IATF 16949:2016), esso può essere definito come una metodologia che, in riferimento ad una determinata attività, operazione, fase o processo caratterizzato da ripetitività, fa ricorso a tecniche statistiche al fine di definire, analizzare e verificare le condizioni che determinano la variabilità dell'oggetto di analisi. In modo più sintetico, rifacendoci alla definizione fornita da Juran potremmo definire l'SPC come "l'applicazione di tecniche statistiche per comprendere ed analizzare le variabilità di un processo".
Obiettivo ultimo quindi, nell'utilizzo di queste tecniche è quello di dotare l'impresa di strumenti adeguati per migliorare il livello dei prodotti/servizi offerti/erogati attraverso l'eliminazione di errori, difformità che causano rilavorazioni, controlli inutili e quindi rallentamenti nei cicli di lavorazione. Garanzia di simili risultati sarà quindi, necessariamente una conoscenza chiara e approfondita dei processi, l'identificazione delle caratteristiche critiche del processo attraverso l'impiego di dati statisticamente significativi e in quanto tali analizzabili che consentano di determinare e interpretare performance e cause che determinano "cambiamenti indesiderati" rispetto al normale funzionamento del processo in analisi. La significatività dei dati e la loro conseguente attendibilità sarà indispensabile al raggiungimento degli obiettivi posti. Non bisogna mai dimenticare, infatti, quello che è il fine ultimo che ci si pone nell'impiegare una metodologia quale SPC: ottenere un efficace supporto per la comprensione di un processo con lo scopo di prevederne l'andamento e intervenire su di esso in tempo reale secondo l'ottica del miglioramento continuo.
Nella pratica aziendale, allora, bisognerà arrivare ad avere dei dati sui cui fondare determinate conclusioni, predisporre azioni che correggano la variabilità di un processo e quindi consentano di risalire dalla manifestazione della variazione "indesiderata" o "anomala" alla causa prima su cui occorre intervenire per modificare le condizioni di svolgimento del processo.
Nell'individuare i fattori che generano tali anomalie e quindi variabilità nel processo in esame si fa sempre riferimento a due categorie principali di cause:
- CAUSE COMUNI
- CAUSE SPECIALI
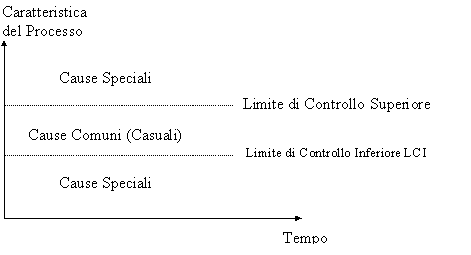
Le cause comuni (o normali) sono insite nella variabilità di un processo produttivo; insorgono casualmente durante il normale svolgimento del processo e ne determinano la fluttuazione naturale all'interno di un intervallo determinato da un limite di controllo superiore e uno inferiore (LCI; LCS - vedi figura);
Alcuni esempi di cause comuni potrebbero essere: la variazione intrinseca di materiali grezzi utilizzati nella linea produttiva, la mancanza di adeguata supervisione, la vibrazione delle macchine e i cambiamenti nelle condizioni lavorative.
Le cause speciali, invece, sono tutte quelle che, come abbiamo già detto, determinano variabilità indesiderata o anomala rispetto al naturale svolgimento del processo. Esse possono derivare, ad esempio, dall’uso di un utensile sbagliato, dall’errore di un operatore o da particolari condizioni ambientali, come l’illuminazione o la temperatura.Fin quando non si provvede ad una loro rimozione o correzione, non si intervenga, cioè, specificatamente su ciascuna, esse continueranno ad influire in maniera imprevedibile sul processo, portandolo fuori controllo.
Un processo si definisce sotto controllo statistico quando la sua variabilità è dovuta solo a cause comuni. Uno stato di controllo statistico, secondo quanto sostiene Deming, non è affatto "uno stato naturale del processo, ma al contrario una conquista fatta per successiva eliminazione una dopo l’altra, di tutte le cause speciali di variabilità". La Variabilità, infatti, è un aspetto ineliminabile in ogni processo produttivo: lo scopo prefissato sarà allora quello di minimizzare le cause di variabilità del processo eliminando, con l’impiego di tecniche statistiche, tutte le cause di tipo speciale.
Una volta individuate e distinte le cause speciali da quelle comuni, dovremo quindi procedere, quando possibile a:
- rimuovere le cause speciali con lo scopo di raggiungere una condizione di stabilità;
- definire quali sono le vie tramite cui realizzare una continua riduzione della variabilità del processo.
Secondo l’approccio del miglioramento continuo, ogni tipo di intervento da sviluppare sul processo di trasformazione, sarà da rapportare non soltanto alle attività già effettuate ma a tutte le attività svolte nel processo, presenti e future,( tenendo ben presenti ostacoli e difficoltà da affrontare nel prevedere in modo attendibile l’andamento futuro dei processi produttivi) considerando che l'SPC è una metodologia orientata alla prevenzione dei difetti e degli errori piuttosto che alla loro semplice scoperta.
Elenchiamo ora tutte le principali tecniche statistiche impiegabili nella metodologia SPC (ci soffermeremo poi sui primi due strumenti: carte di controllo e analisi della capability):
- Carte di controllo per variabili
- Carte di controllo per attributi
- Carte di controllo multivariate
- Analisi della capability
- Benchmarking
- Foglio raccolta dati
- Foglio di verifica
- Diagramma di Pareto
- Stratificazione
- Diagramma causa-effetto
- Istogramma di fequenza
- Ripetibilità e riproducibilità
- Diagramma di correlazione
Accenniamo solo ad alcuni dei possibili impieghi di questi strumenti:
- Previsione della possibilità di raggiungere le tolleranze di progetto;
- Pianificazione di verifiche dei controlli di processo;
- Analisi di possibili interdipendenze tra i processi;
- Interventi correttivi durante la lavorazione;
- Valutazione di nuove attrezzature;
- Elaborazione di specifiche.
Molti altri evidentemente ve ne sono associabili alle differenti tecniche, giustificanti quindi l'impiego e la scelta di uno strumento piuttosto che dell'altro.
Gli studi sull'SPC non sono certo temi nuovi alla Qualità. Già nel 1924, infatti, il dott. W.A. Shewart iniziò a sviluppare un approccio statistico al controllo Qualità rilevando che il concetto di variabilità riferito ai fenomeni naturali era parimenti adeguato all'analisi e alla descrizione dei processi produttivi. Con il contributo della statistica inferenziale e della statistica descrittiva, arrivò allora alla descrizione sintetica di fenomeni più ampi da impiegare come modelli di supporto alle attività di Problem Solving. Nacquero così le sue Carte di controllo uno degli strumenti statistici più impiegati nell'analisi dei processi produttivi. Da allora i passi avanti compiuti sul tema sono stati molti. Primo fra tutti il riconoscimento circa la validità di questi strumenti e un loro più vasto impiego. Il controllo Statistico della Qualità ha cessato di essere semplicemente un supporto al cosiddetto "Scientific Management" per divenire strumento diffuso da collocare all'interno di un vero e proprio approccio di gestione/organizzazione. In quest'ambito, le metodologie SPC seppur a livelli differenti di approfondimento devono comunque divenire patrimonio aziendale comune e condiviso a tutti i livelli. Va cioè diffondendosi all'interno dell'organizzazione un orientamento finalizzato a coniugare l'approccio tradizionale ai problemi con un approccio fondato sullo Statistical thinking come atteggiamento culturale. Va sottolineato, tuttavia, come ciò debba valere non solo per ruoli tecnici piuttosto che manageriali, ma anche e soprattutto per coloro che, in quanto operatori, possono incidere direttamente sul proprio processo attraverso un'analisi che si configura come un vero e proprio Learning by doing. Occorre ricordare, infatti, quali possono essere i vantaggi ottenibili da un corretto impiego di metodologie di tipo SPC per capire come essi interessino tutta la struttura aziendale e richiedano, quindi, il coinvolgimento e il supporto di ciascuno:
- maggiore uniformità della qualità del prodotto;
- possibilità di bloccare i difetti al loro insorgere;
- minori spese di collaudo;
- riduzione degli scarti e delle riprese di lavoro;
- diffusione tra il personale di un giusto apprezzamento della qualità;
- migliori relazioni con la clientela;
- individuazione rapida delle cause di difetti;
- individuazione dei limiti delle macchine;
- determinazione preventiva della quantità ottenibile.
Queste considerazioni non sono ridondanti; al contrario risultano necessarie nel momento in cui si è in fase di definizione della strategia di implementazione di un programma di SPC dato che evidenziano la necessità di coinvolgere non solo le funzioni di produzione e di controllo qualità ma anche le funzioni organizzative e di gestione delle risorse umane per assicurare al programma stesso efficacia e coerenza con i fabbisogni dei processi, ma, anche e soprattutto, con la dimensione culturale, organizzativa e strategica dell'organizzazione.
Dopo queste necessarie premesse potremmo iniziare con la presentazione del principale strumento cui si ricorre nell'implementazione di un Controllo Statistico di Processo le Carte di Controllo.
LE CARTE DI CONTROLLO
La prima Carta di Controllo fu proposta, come abbiamo già accennato, il 16 maggio 1924 da Walter A. Shewhart, allora capo dei Laboratori Bell, che in una nota al capo del Dipartimento di Ingegneria Ispettiva della Western Electric scriveva:
"il modello di rapporto allegato è stato progettato per indicare se le variazioni osservate nella percentuale di apparati difettosi siano o no significative, a indicare cioè se il processo sia soddisfacente."
Il rapporto allegato divenne in seguito noto come la prima Carta di Controllo di Shewhart, ed iniziò così l’era del Controllo Statistico di Qualità [1].
Come introdotto precedentemente, le Carte di Controllo rappresentano un valido strumento per comprendere se un processo è statisticamente sotto controllo, e, se non lo è, danno una valida indicazione del motivo del fuori controllo.
In generale le Carte di Controllo possono essere definiti strumenti grafici di controllo continuo e in linea del processo, del quale forniscono una rappresentazione grafica dell’evoluzione temporale.
Del processo sotto esame vengono raccolti dai campioni i dati necessari e da questi sono ricavati i parametri statistici come media, deviazione standard, o il range. Essi sono poi riportati sulle Carte. Queste operazioni vengono compiute per un certo numero di campioni, dopo di che la Carta è pronta per essere letta e interpretata.
Benefici delle carte di controllo
Le Carte di Controllo forniscono importanti informazioni sul processo produttivo. Permettono di capire:
-
Quando intraprendere le azioni correttive, e quando lasciare seguire al processo il suo naturale sviluppo;
Se da una parte infatti la Carta di Controllo indica il comportamento anomalo di un processo che rende necessaria una azione correttiva, dall’altra evita controlli superflui o continue regolazioni del processo che avrebbero l’effetto indesiderato di aumentarne la variabilità. -
Quale tipo di azioni correttive sono necessarie e il reale effetto che hanno avuto sul processo;
Ciò è reso possibile dall’analisi e dall’interpretazione delle configurazioni risultanti dalle Carte. Inoltre, se utilizzate in tempo reale mediante l’acquisizione informatizzata dei dati, forniscono una retroazione istantanea sulle prestazioni del processo. -
La capacità reale del processo e i mezzi per migliorarlo;
Quando il processo si trova in stato di controllo statistico è possibile valutarne la reale efficienza produttiva e la capacità di rientrare nelle specifiche richieste, e quindi di soddisfare il cliente. Se il processo non dovesse mostrarsi idoneo si potrebbe migliorarlo, ad esempio, ricorrendo all’eliminazione delle Cause Comuni.
Tipi di carte di controllo : carte per variabili e per attributi
Le carte di controllo si dividono in due categorie in base al tipo di dati, dati variabili e dati attributi, estrapolati dall’analisi del processo in esame e sui quali sono costruite. Si hanno le Carte per Variabili e le Carte per Attributi. I dati variabili hanno le seguenti proprietà :
- Sono misurabili su una scala numerica tramite unità di lunghezza, diametro, peso, temperatura, ecc.;
- Sono continui. L’accuratezza della loro misura dipenderà perciò dalla risoluzione dello strumento di misura;
- Se riferiti alla stessa unità di misura, possono essere confrontati numericamente, permettendo di ricavare informazioni come media e dispersione.
I dati attributi, invece, hanno una o più delle seguenti caratteristiche:
- Sono enumerabili. Possono, cioè, indicare la presenza o l’assenza di una condizione, come ad esempio i difetti di lavorazione
- Sono classificabili o graduabili usando una scala, che valuti la gravità dei difetti;
- Sono dati del tipo "passa/non passa", e non possono dunque fornire indicazioni sulla variabilità del processo, l’indicatore principale del suo miglioramento.
I dati attributi possono inoltre essere classificati come non conformità (totale, percentuale ecc.), o non conformi.
La non conformità è la non rispondenza di un certo attributo dell’oggetto prodotto alle specifiche date, mentre è non conforme un prodotto che non risponde alle proprietà complessive.
Un pezzo non conforme potrà dunque essere caratterizzato da una o più non conformità.
Il numero di dati necessari per la compilazione di una Carta per Attributi é quindi minore del numero di dati necessari a una Carta per Variabili; queste ultime forniscono però un maggior numero di informazioni delle Carte per Attributi.
Nella seguente tabella sono riportati i differenti tipi di Carte di Controllo con riferimento al tipo di dati trattato e al parametro del processo sotto controllo.
| Tipo di Dati | Tipo di Carta | Parametro del processo sotto controllo |
|---|---|---|
| x medio | media | |
| Variabili | \(R\) | dispersione |
| \(s\) | dispersione | |
| \(X\) | valori individuali | |
| \(p\) | frazione di non conformi | |
| Attributi | \(np\) | numero di non conformi |
| \(c\) | numero di non conformità | |
| \(u\) | numero di non conformità per unità |
TAB.1 : Carte di Controllo con riferimento al tipo di dati trattato e al parametro del processo sotto controllo.
Combinazione delle carte per variabili
A differenza delle Carte per Attributi le Carte per Variabili sono sempre utilizzate in coppia (combinazione). Una di esse controlla la media del processo (Carta x medio), l’altra la dispersione (Carta R o Carta s). La combinazione delle Carte di Controllo aumenta la possibilità di individuare un processo fuori controllo e, rispetto alla Carta singola, fornisce una maggiore quantità di informazioni utili per eliminare le Cause Attribuibili. Per questo motivo si parla di Carta x medio - R o di Carte x medio - s come se si trattasse di una carta sola.
Breve descrizione delle carte
Esistono vari tipi di Carte di Controllo, sia di quelle per Variabili che per Attributi, caratterizzate da funzioni e modalità di utilizzo e compilazione tra loro differenti. Se ne descrivono qui di seguito le principali caratteristiche.
-
Carta x medio - R
Le Carte x medio e le Carte R sono le più utilizzate nel controllo e nell'analisi delle variabili di un processo. Le misurazioni inerenti ad una specifica caratteristica del processo sono raccolte in campioni di limitate dimensioni, generalmente da due a sei per ogni campione. La costruzione di una Carta x medio - R richiede i seguenti passi:
- selezione della grandezza e del numero dei campioni e della frequenza di campionamento;
- raccolta dei dati per il periodo di tempo di interesse;
- calcolo della media e del range R per ogni campione;
- rappresentazione grafica delle medie e dei range sulla Carta;
- calcolo del Limite Centrale (LC) e dei Limiti di Controllo Superiore ed Inferiore (LCS e LCI) e rappresentazione sulla carta;
- studio della configurazione dei punti sulla Carta in relazione ai limiti calcolati.
-
Carta x medio - s
Anche le carte x - medio e le carte s sono usate in congiunzione. Lo Scarto campionario s è un indicatore molto efficiente della variabilità di un processo, specialmente per campioni di grandi dimensioni, ma è meno facile da calcolare e meno sensibile alle Cause Attribuibili di Variabilità che determinano l'anomalia di un unico valore in un campione ; il range, infatti, definito come la differenza tra il valore massimo e il minimo dei valori all’interno di un campione, mette bene in evidenza valori che si allontanano eccessivamente dagli altri. La modalità di realizzazione di tale Carta è analoga a quella della Carta x medio - R, eccetto il punto 3 che diventa il seguente:
- calcolo di s, di s medio, e dei Limiti di Controllo per le due Carte.
-
Carta X
A differenza delle Carte precedenti che raggruppano e valutano campioni di dati composti da diversi individui, le Carte X (spesso indicate col nome di Carte per gli Individui), sono caratterizzate dall'analisi di quantità individuali di misure. Ogni campione è cioè composto di un unico elemento, situazione tipica delle procedure di raccolta dati molto costose o di prove distruttive, o quando il tempo di fabbricazione è molto lungo. Per una Carta X l’indice di dispersone viene calcolato utilizzando la variazione mobile (moving range), definita come il valoreassoluto della differenza tra due osservazioni successive. L’utilizzo di una Carta X-Moving Range deve essere sempre accompagnato da uno studio della distribuzione di probabilità dei campioni, per valutare che sia di tipo gaussiano. Non calcolando medie, infatti, il Teorema del Limite Centrale non è applicabile, a differenza delle Carte precedenti. I passi necessari per la creazione di una Carta X sono i seguenti:
- Analisi della distribuzione dei campioni;
- Raccolta dei dati per il periodo di tempo di interesse;
- Calcolo della media dei valori raccolti;
- Calcolo della variazione mobile per i dati in ordine di raccolta;
- Calcolo della media delle variazioni, della deviazione standard e dei relativi Limiti di Controllo;
- Rappresentazione grafica dei limiti e studio delle configurazioni.
-
Carta c
La Carta c è quella principalmente utilizzata nell'analisi dei dati di tipo attributo, per il conteggio di un certo evento su periodi consecutivi di tempo. Il suo sviluppo richiede i passi seguenti:
- Raccolta dei dati per il periodo di interesse;
- Calcolo del Limite Centrale;
- Calcolo e tracciamento dei Limiti di Controllo Superiore e Inferiore;
- Studio delle configurazioni ottenute.
-
Carta u
Le Carte u, dette anche Carte di velocità, sono utilizzate per campioni formati da un numero variabile di elementi. I passi da seguire per la costruzione di una Carta u sono gli stessi della Carta c, ma i Limiti di Controllo sono diversi per ciascun campione.
-
Carte p
Le Carte p, o Carte di proporzione, vengono utilizzate per mostrare la frazione di non conformi di un campione di grandezza variabile. La modalità di costruzione è la stessa della Carta u, compreso il calcolo dei Limiti che deve essere svolto per ciascun intervallo di tempo essendo la dimensione dei campioni variabile.
-
Carte np
Come le Carte p, la Carta np è utilizzata nell'analisi del numero di non conformi nel caso in cui il numero di campioni sia costante. La costruzione è analoga a quella della Carta p.
COMPONENTI DELLE CARTE. La compilazione di una Carta di Controllo non richiede solo il calcolo dei Limiti di Controllo, ma presuppone un’attenta analisi dei problemi derivanti dalla selezione dei campioni e degli elementi di ogni campione nonché dalla frequenza di campionamento. Per ognuno di questi è però possibile fornire dei criteri di scelta. Di seguito riporteremo quelli relativi al calcolo dei limiti. Sulla Carta di Controllo vengono sempre indicati tre Limiti di Controllo, rappresentati da altrettante linee: il Limite Centrale LC, e i Limiti di Controllo Superiore LCS ed Inferiore LCI. Essi hanno il compito di fornire un aiuto alla lettura della Carta e alla sua interpretazione. Essi soddisfano le seguenti relazioni: \(LCS = m + ks\), \(LC = m\), \(LCI = m - ks\) dove \(m\) e \(s\) sono, rispettivamente, la media e lo scarto di uno specifico processo, e \(k\) una costante che può assumere i valori ± 1, ± 2, ± 3. I limiti LCS e LCI veri e propri sono ricavati con k = ± 3 , mentre gli altri due valori di k indicano due limiti che dividono la carta in tre diverse zone, come mostrato in Fig.4 - 2.

- La zona A corrisponde ad una area compresa tra 2 e 3 scarti dalla media del processo; la probabilità che un punto cada in tale zona è \(P(A)=2·0,0213=0,0426\);
- La zona B corrisponde ad una area compresa tra 1 e 2 scarti e la probabilità associata è di \(P(B)=2·0,1360=0,2720\);
- La zona C corrisponde ad una area compresa tra la media del processo ed uno scarto, e la probabilità che un punto vi cada è pari a \(P(C)=2·0,34130=0,6826\);
- Infine la probabilità che un punto cada al di fuori dei limiti superiore ed inferiore LCS e LCI vale \(P(D)=2·0,00135=0,00270\).
Tali valori sono ricavati dallo studio delle proprietà della densità di probabilità di una gaussiana. Si può comunque notare che la somma delle tre probabilità associate alle zone A, B, e C è un valore molto vicino a 1.
\(P_{SOM}=P(A)+P(B)+P(C)=0,0426+0,2720+0,6826=0,9972\), che può essere visto come \(P_{SOM}=1-2P(D)=1-0,0027=0.9973\) dove 1 è la probabilità totale. I limiti LCS e LCI sono scelti in modo tale che la probabilità che i punti ottenuti dai dati forniti dai campioni cadano al loro interno sia quasi uno se il processo è sotto controllo statistico (l’evento certo ha probabilità uno). Il punto rappresentativo di un campione cade perciò entro i limiti LCS e LCI il 99,74% delle volte se il processo è sotto controllo, ed è quindi governato esclusivamente dalle Cause Comuni. Se invece cade fuori dai limiti di controllo è probabile che all’interno del nostro processo sia presente una Causa Attribuibile: è dunque necessario indagarne l’origine.
Lettura delle carte di controllo
L’analisi e l'interpretazione delle Carte di Controllo è uno dei momenti più delicati e importanti del Controllo Statistico di un processo : un’errata lettura delle Carte può rendere inutile la raccolta dei dati compiuta fino a quel momento, o, peggio ancora, può indurre azioni correttive non necessarie o evitare correzioni di un processo fuori controllo con conseguente spreco di risorse umane ed economiche. Chi è preposto alla lettura delle Carte deve quindi poter riconoscere in modo univoco i comportamenti anomali del processo, così da apportarvi le opportune modifiche avvalendosi dei criteri di interpretazione delle Carte di Controllo. Come già spiegato in precedenza, la costruzione delle Carte di Controllo si basa sull’analisi statistica di un processo: ciò le rende soggette ad un certo grado di incertezza, del quale è sempre necessario tenere conto, e che può essere aumentato o diminuito agendo sul posizione dei Limiti di Controllo sulla carta.
Tipi di errore nell'interpretazione delle carte di controllo
Si definiscono due errori di interpretazione, gli Errori di Tipo I e gli Errori di Tipo II:
- L’Errore di Tipo I si commette quando si suppone che un processo sia fuori controllo statistico mentre in realtà è sotto controllo. La probabilità di commettere un errore di Tipo I è indicata con a.
Come esempio si consideri un processo sotto controllo, tale cioè che sia governato solo da un insieme di Cause Comuni. Se la misura di un campione dovesse cadere oltre i Limiti Superiore ed Inferiore, si potrebbe ipotizzare che il processo è fuori controllo. Tuttavia, essendo i limiti ad una distanza finita dal Limite Centrale (generalmente a ± 3s ), una probabilità seppur piccolissima che ciò avvenga esiste, e vale \(P(D)=2·0,00135=0,0027\). In tale caso considerare il processo fuori controllo è sbagliato.
-
L’Errore di Tipo II si commette considerando il processo sotto controllo quando in realtà non lo è. Graficamente nessuna osservazione cade al di fuori dei limiti di controllo : ciò porta ad assumere che siano presenti esclusivamente Cause Comuni.
Si supponga, tuttavia, che il processo sia in realtà fuori controllo. Ciò può accadere, ad esempio, per una variazione nella media o nella variabilità del processo, dovute ad un cambiamento nella profondità di taglio da parte di un operatore, o in un diversa qualità di materiali grezzi utilizzati o ancora alla presenza di un nuovo operatore, ecc. Sotto tali circostanze è ancora fortemente probabile che una osservazione cada entro i Limiti di Controllo.
Compilazione della carta x medio - R
La Carta x medio - R è la Carta per Variabili maggiormente utilizzata. Essa è composta da due Carte: la Carta x medio per il controllo della media del processo e la Carta R per il controllo della variabilità del processo, tramite l'indice statistico R o Range. La grande diffusione della Carta x medio - R rispetto alla Carta x medio - s è dovuta alla facilità dei calcoli necessari alla sua compilazione. Tutte le scelte che è necessario fare prima di cominciare la compilazione vera e propria di una Carta di Controllo costituiscono le operazioni preliminari . Dalla linea di produzione del processo in esame vengono prelevati n elementi consecutivamente: essi formano il primo campione. Tale operazione viene ripetuta m volte ad intervalli fissi, formando così m campioni. La regola generale è di cercare di minimizzare la variabilità all’interno dei campioni e di massimizzarla tra i campioni. Inoltre i lotti da cui i campioni sono estratti devono essere omogenei, quindi la Carta di Controllo dovrà essere esclusiva per ogni macchina, operatore, e così via. La regola pratica è di scegliere come grandezza dei campioni \(n=5\), e come numero dei campioni \(m=20,25\). Queste quantità possono variare a seconda che il processo sia o meno sotto controllo. I passi da seguire nella compilazione della Carta x medio R sono i seguenti:
- Lo schema prestampato di una Carta di Controllo viene compilato nella parte riguardante i dati generici del processo (come il tipo di prodotto, il numero di disegno, il numero e il tipo di operazione compiuta, il numero della macchina, ecc.), e con l’avanzare del processo, anche nella parte dei dati raccolti (che per questa Carta sono misure di una caratteristica del prodotto sotto esame: ad esempio il diametro, la resistenza elettrica, ecc.).
- Si calcola la media \(\overline{x_{i}}\) e il range \(R_i\) per ognuno degli \(m\) campioni presenti:
\[\overline{x_{i}}= \frac{\sum\limits_{i=1}^n x_i}{n}\]
\(R_i=x_{i\max}-x_{i\min}\) dove gli \(x_i\) sono i valori misurati per ogni \(n\) elemento, e \(x_{i\max}\) e \(x_{i\min}\) sono rispettivamente il valore massimo e il valore minimo misurato in ogni campione. Si calcola il Limite Centrale per la Carta x medio e per la Carta R:
\[LC_X=\overline{\overline{x}}=\frac{\sum\limits_{i=1}^m \overline{x_i}}{m}\]
\[LC_R=\overline{R}=\frac{\sum\limits_{i=1}^m R_i}{m}\]
Si calcolano i Limiti di Controllo Superiore ed Inferiore per entrambe le Carte. Teoricamente \(LCS_X\) e \(LCI_X\) dovrebbero essere posizionati a \(LC_{X}\pm 3 s_X\), dove \(s_x\) rappresenta la deviazione standard della media dei campioni. Il calcolo di questa quantità, soprattutto per \(m\) e \(n\) alti, è complesso e suscettibile di errori. Si usa allora una stima \(\widetilde{\sigma}\) della deviazione standard del processo, e da questa, per il Teorema del Limite Centrale si ricava \(s_x\).
\[\widetilde{\sigma} = \frac{\overline{R}}{d_2} \]
\[\sigma_X=\frac{\sigma}{\sqrt{n}} \cong \frac{\widetilde{\sigma}}{\sqrt{n}}= \frac{\overline{R}}{d_2*\sqrt{n}}\]
dove \(d_2\) è un parametro che si ricava dalle apposite tabelle e che dipende da \(n\). I Limiti per la Carta x medio diventano quindi:
\[LCS_X,LCI_X=LC_X\pm3\sigma_X=LC_X\pm3\frac{\overline{R}}{d_2*\sqrt{n}}=LC_X\pm A_2\cdot\overline{R} \]
dove \(A_2= \dfrac{3}{d_2*\sqrt{n}} \) si ricava dalle tabelle (cfr.App.1). Il procedimento è analogo per il calcolo di \(LCS_R\) e \(LCI_R\).
\[LCS_R,LCI_R=\overline{R}\pm 3\sigma_{R} \]
Essendo \(R=s \cdot W\) e \(s_R=s\cdot s_W\) ed effettuando una stima, si ricava che \(\widetilde{\sigma}_R=\widetilde{\sigma}\cdot \widetilde{\sigma}_W\ = \widetilde{\sigma} \cdot d_3\)
Inoltre, dalla relazione \(\widetilde{\sigma}= \dfrac{\overline{R}}{d_2}\) si ottiene: \(\widetilde{\sigma}_R=\dfrac{\overline{R}}{d_2}d_3\)
I Limiti della Carta R diventano così : \[LCS_R=\overline{R}+ 3 \frac{\overline{R}}{d_2} d_3 = \overline{R}\cdot\left( 1+3\frac{d_3}{d_2}\right) = \overline{R}\cdot D_4 \] \[LCI_R=\overline{R}- 3 \frac{\overline{R}}{d_2} d_3 = \overline{R}\cdot\left( 1-3\frac{d_3}{d_2}\right) = \overline{R}\cdot D_3 \] dove i valori \(D_3\) e \(D_4\) sono riportati nelle opportune tabelle (cfr.App.1). - I Limiti ricavati vengono disegnati sulla Carta.
- La prima Carta che viene letta è la Carta R. Su di essa, e più precisamente sul parametro \(\overline{R}\), si basa infatti il calcolo di\(LCS_X\) e \(LCI_X\). Se la Carta R mostra un segnale di fuori controllo, allora la Carta x medio potrebbe non essere affidabile e quindi non va interpretata: è necessario intraprendere prima le azioni correttive necessarie ad eliminare le cause di fuori controllo della Carta R.
- Una volta determinata la causa del fuori controllo si ricalcolano i Limiti di Controllo Centrale, Superiore ed Inferiore, sia per la Carta x medio che per la Carta R, eventualmente eliminando dal calcolo i campioni ai quali corrispondono punti oltre detti Limiti.
- I nuovi limiti sono chiamati Limiti di Controllo Corretti (o Modificati).
- Le Carte possono ora essere di nuovo lette alla ricerca di eventuali Cause Attribuibili. Nel caso ne venissero individuate di nuove si ritorna al punto precedente. In caso contrario si può concludere che il processo è sotto controllo statistico.
Carte x medio - R con limiti di controllo predefiniti
Come accennato, le Carte di Controllo possono essere utilizzate per determinare se un processo può essere realizzato con i mezzi a disposizione dell’azienda. In tal caso i Limiti di Controllo saranno predefiniti dalla direzione che indicherà i valori di media e di deviazione standard entro i quali il processo deve mantenersi. La compilazione delle Carte avverrà allora in modo diverso da quello appena analizzato Supponiamo che \(X_0\) e \(s_0\) siano rispettivamente la media e la deviazione standard imposti. I Limiti Centrale, Superiore ed Inferiore per la Carta x medio sono:
\(LC_X=X_0\), \(LCS_X,LCI_X=X_0 \pm 3 \dfrac{\sigma_0}{\sqrt{n}} = X_0 \pm A \cdot \sigma_0\) dove \(A=\dfrac{3}{\sqrt{n}}\) si ricava dalle apposite tabelle (cfr. App.1).
Essendo \(\widetilde{\sigma} = \dfrac {\overline{R}}{d_2} \Rightarrow \overline{R} = d_2+\widetilde{\sigma}\) e \(\widetilde{\sigma} = \sigma_0\) per la Carta R si ha che :
\(LC_R = \overline{R}= d_2*\widetilde{\sigma}=d_2+\sigma_0\)
Limiti Superiore ed Inferiore sono ricavati considerando che \(\sigma_R=d_3*\sigma\) e \(\sigma \cong \sigma_0\), e valgono:
\[LCS_R = \overline{R}+3\sigma_{R}=d_2\cdot \sigma_0 + 3 \cdot d_3 \cdot \sigma_0 = \sigma_0 \cdot (d_2+3d_3) = \sigma_0 \cdot D_2\]
\[LCI_R = \overline{R}-3\sigma_{R}=d_2\cdot \sigma_0 - 3 \cdot d_3 \cdot \sigma_0 = \sigma_0 \cdot (d_2-3d_3) = \sigma_0 \cdot D_1\]
con \(D_2\) e \(D_1\) deducibili dalle tabelle. L’interpretazione della Carta con Limiti Predefiniti avviene in modo differente dalla precedente. Se uno o più punti cadono oltre i Limiti di Controllo, ciò non è necessariamente dovuto all'effetto di Cause Attribuibili, ma gli obiettivi posti potrebbero non essere realistici per il processo che li deve realizzare: in questo caso si cercherà di agire sulle Cause Comuni per far rientrare il processo nelle specifiche e, se questo non è possibile, si cambierà il processo.
Carta x medio - S. Generalità: quando il numero n dei componenti i campioni è maggiore di 10 alla Carta R si preferisce la Carta s. Il range R infatti, calcola la variabilità di un campione semplicemente come la differenza tra il campione di valore più alto e quello di valore più basso. Quando il numero dei campioni diventa alto questo tipo di stima risulta impreciso, e si deve ricorrere al calcolo della deviazione standard s. La deviazione standard è un indice che tiene conto di quanto i valori che costituiscono una certa popolazione o campione differiscono dal valore medio. In generale essa è espressa dalla relazione
\[\sigma=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n(x_i-\mu)^2}\]
dove \(n\) indica il numero di componenti la popolazione, \(x_i\) l'i-esimo elemento, e \(\mu=\overline{x_i}\) la media della popolazione. Se consideriamo invece i campioni e non la popolazione, allora per il calcolo della deviazione standard si preferisce utilizzare una forma leggermente diversa:
\[s=\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^n(x_i-\mu)^2}\]
Esistono poi altre due importanti relazioni che verranno utilizzate in seguito:
\[E(s)=c_4\cdot \sigma \, \, \, \,\,\,\, \sigma_s = \sigma \cdot \sqrt{1-{c_4}^2}\]
La prima relazione indica che il valor medio E(s) della deviazione standard s dei campioni è proporzionale alla deviazione standard s della popolazione tramite il parametro \(c_4\), che dipende dalla numerosità dei campioni \(n\) ed è tabulato. La seconda relazione pone invece in relazione la deviazione standard \(sigma_s\) delle deviazioni standard dei campioni, con quella della popolazione \(\sigma\)
Compilazione della Carta x medio - s: i passi da seguire sono gli stessi della Carta x medio - R. I l Limite Centrale della Carta s è dato da
\[LC_S=\overline{{s}}=\frac{\sum\limits_{i=1}^m {s_i}}{m}\]
dove \(s_i\) è la deviazione standard di ognuno degli \(m\) campioni, mentre i Limiti Superiore ed Inferiore sono
\[LCS_S,LCI_S=\overline{s} \pm 3 \sigma_S = \overline{s} \pm 3 \sigma \cdot \sqrt{1-{c^2_4}}\]
Essendo \(s\), la deviazione standard della popolazione, sconosciuta, essa viene stimata tramite la relazione \(E(s)=c_4\cdot \sigma\), cioè \(\widetilde{\sigma}=\dfrac{\overline{s}}{c_4}\).
I Limiti Superiore ed Inferiore diventano:
\[LCS_S,LCI_S=\overline{s} \pm 3 \frac{\overline{s}}{c_4} \cdot \sqrt{1-{c^2_4}} = \overline{s} \left( 1 \pm 3 \frac{1}{c_4}\cdot \sqrt{1-c^2_4}\right)\]
Definendo
\[B_4=1 + 3 \frac{1}{c_4}\cdot \sqrt{1-c^2_4}\]
\[B_3=1 - 3 \frac{1}{c_4}\cdot \sqrt{1-c^2_4}\]
si ottiene che \(LCS_S=B_4\cdot \overline{s}\) e \(LCI_S=B_3\cdot \overline{s}\), con \(B_4\) e \(B_3\) tabulati.
I Limiti della Carta x medio sono:
\[LC_X=\overline{\overline{x}}=\frac{\sum\limits_{i=1}^m \overline{x_i}}{m}\]
Le regole di costruzione e di interpretazione della Carta x medio - s sono le stesse della Carta x medio - R. Si dovrà perciò costruire ed interpretare prima la Carta s, e ,se questa risulta sotto controllo, costruire ed interpretare la Carta x medio, con \(A_3=3\dfrac{1}{c_4\cdot \sqrt{n}}\) tabulato.
Limiti di controllo predefiniti: siano \(X_0\) e \(s_0\) rispettivamente il valor medio e la deviazione standard assegnati entro i quali il processo deve rientrare. Allora si ha:
\(LCS=c_4\cdot a_0\)
\[LCS_S,LCI_S=\overline{s} \pm 3 \sigma_S = c_4 \cdot \sigma_0 \pm 3 \sigma_0 \cdot \sqrt{1-c^2_4} = \sigma_0 \cdot \left( c_4 \pm 3 \cdot \sqrt{1-c^2_4}\right)\]
Definendo:
\[B_6 = c_4 + 3 \cdot \sqrt{1-c^2_4}\]
\[B_5 = c_4 - 3 \cdot \sqrt{1-c^2_4}\]
si ottiene: \(LCS_S=B_6 \cdot \sigma_0\) e \(LCI_S=B_5 \cdot \sigma_0\)
I Limiti per la Carta x medio sono invece: \(LC_X=X_0\) e \(LCS_X,LCI_X = X_0 \pm 3 \dfrac{\sigma_0}{\sqrt{n}} = X_0 \pm A \cdot \sigma_0\)
come visto in precedenza.
COMPILAZIONE DELLA Carta X: La Carta X, o Carta per gli Individui, viene usata quando la numerosità dei campioni non può essere maggiore di uno. Il problema che si pone è allora di determinare la variabilità del processo. Ciò viene fatto per mezzo della variazione mobile o moving range, \(MR_i\), definita nel seguente modo: \(MR_i=|x_{i+1}-x_i|\)
dove \(x_{i+1}\) è la misura presente e \(x_{i}\)è la misura precedente. Se i campioni sono \(m\) il numero dei moving range è \(m-1\) (\(MR_1\) non esiste). Poiché gli \(m-1\) moving range sono correlati tra loro, si dovrà fare particolare attenzione ai calcoli e all’interpretazione della Carta.
Compilazione della Carta:
Il Limite Centrale per la Carta moving range è dato da:
\[LC_{MR}=\overline{MR}=\frac{\sum\limits_{i=1}^{m-1} MR_i}{m-1}\]
mentre i Limiti Inferiore e Superiore sono espressi dalle relazioni seguenti: con considerazioni analoghe a quelle fatte per la Carta R. Quindi
\(LCS_{MR}=D_4\cdot LC_{MN}\) e \(LCI_{MR}=D_3\cdot LC_{MN}\)
dove \(D_4\) e \(D_3\) vengono dedotti dalle tavole per \(n=2\), e valgono rispettivamente 3,267 e 0. I Limiti per la Carta X sono :
\[LC_{X}=\overline{X}=\frac{\sum\limits_{i=1}^{m} X_i}{m}\]
\[LCS_X=\overline{X}+3\cdot \frac{\overline{MR}}{d_2}\]
\[LCI_X=\overline{X}-3\cdot \frac{\overline{MR}}{d_2}\]
Tali relazioni sono state ottenute assumendo come stima della deviazione standard del processo \(\widetilde{\sigma}=\dfrac{\overline{MR}}{d_2}\) con \(d_2\) che vale 1,128 per \(n=2\).
Limiti di Controllo Predefiniti detti \(X_0\) e \(s_0\) sono rispettivamente la media e la deviazione standard assegnati, i Limiti Predefiniti per la Carta X sono:
\[LC_X=X_0, \,\,\, LCS_X=X_0+3\sigma_0, \,\,\, LCI_X=X_0-3\sigma_0\]
mentre per la Carta moving range si ricava che:
\[LC_{MR}=d_2\cdot \sigma_0, \,\,\, LCS_{MR}=D_4d_2\sigma_0=(3,267)\cdot(1,128)\cdot\sigma_0=3,685\cdot\sigma_0, \,\,\, LCI_{MR}=D_3d_2\sigma_0=(0)\cdot(1,128)\cdot \sigma_0=0\]
Analisi della capacità
Indici di capacità del processo: le Carte di Controllo sono un potente mezzo per mantenere un processo sotto controllo statistico, indicando le azioni correttive che devono essere intraprese al fine di eliminare le cause di variabilità indesiderata, le Cause Attribuibili. Le Carte di Controllo non tengono conto, però, delle specifiche a cui il processo deve attenersi, come ad esempio le tolleranze di lavorazione o altre caratteristiche richieste al prodotto in output al processo. Il loro utilizzo non è dunque sufficiente a comprendere la reale capacità di un processo, né come questo può essere migliorato. A questo scopo vengono definiti gli indici di capacità del processo, che mettono in relazione le prestazioni o il potenziale del processo con il soddisfacimento a specifiche imposte. Essi, inoltre, permettono di riassumere in modo molto conciso i dati di un processo produttivo, con il vantaggio, rispetto agli indici statisti come media e dispersione, di essere quantità adimensionali, e quindi facilmente interpretabili e paragonabili tra loro. Un miglioramento della capacità dei processi si può ottenere attraverso una riduzione del numero e dell'effetto delle Cause Attribuibili, nonché della ricerca della "centratura" del processo stesso. In generale la capacità di un processo:
- dipende dai limiti specificati
- è valutata per ogni caratteristica
- dipende dalla dispersione del processo
- dipende dalla posizione del processo
- si determina con l'uso delle carte di controllo o con un’analisi specifica
- si può valutare attraverso gli indici di capacità
Gli indici più comunemente usati sono il Cp e il Cpk. L’utilizzo di questi indici risulta particolarmente comodo se fatto in congiunzione con le Carte di Controllo. Altrimenti, oltre a dover raccogliere appositamente i dati, è anche necessario assicurarsi che la popolazione da cui tali dati sono prelevati sia distribuita secondo una funzione normale, perché è in relazione ad essa che Cp e Cpk sono definiti. La verifica della distribuzione di un insieme di elementi può essere fatta tramite istogrammi o diagrammi in scala gaussiana, analogamente allo studio dell’applicabilità delle Carte per Individui.
Indice Cp: Cp è l’indice che misura il "potenziale del processo" ed è definito come : \[Cp=\frac{LTS-LTI}{6\sigma}\] dove LTS e LTI indicano rispettivamente il Limite di Tolleranza Superiore e il Limite di Tolleranza Inferiore e s la deviazione standard del processo. Cp è dunque la misura del rapporto tra la dispersione ammissibile per il processo, calcolata dalla differenza tra i Limiti di Tolleranza, e la dispersione reale, rappresentata dal valore 6s, detta anche Tolleranza Naturale, TN [11]. Si utilizza 6s perché in una distribuzione gaussiana, come si suppone che sia quella sotto esame, il 99,73% degli elementi è compreso in sei volte la deviazione standard, quando si hanno esclusivamente variazioni casuali. Per questo motivo la capacità di processo può essere calcolata solamente se il processo è stabile (non sono, cioè, presenti Cause Attribuibili), ed è distribuito normalmente. Cp è un buon indicatore della Capacità di Processo, ma da solo può non essere sufficiente ; esso infatti controlla solo la dispersione del processo, senza fornire alcuna informazione sulla sua centratura. È infatti possibile che un alto valore di Cp, che dovrebbe indicare un processo piuttosto capace, produca in realtà un alto numero di scarti a causa della deriva della media del processo vicino ai limiti di tolleranza. Cp indica dunque quanto un processo è "capace" solo se è centrato. Per questo motivo si introduce l’indice Cpk, che considera anche la posizione del processo rispetto ai Limiti di Tolleranza.
Indice Cpk: Cpk è l’indice che misura la "prestazione del processo". Esso misura sia la dispersione che la centratura del processo, tenendo conto dell’ampiezza della distribuzione e della posizione in cui è posta, rispetto al punto medio della specifica. Viene definito come : \[Cpk=\min{\left\{\frac{LTS-\mu}{3\sigma},\frac{\mu-LTI}{3\sigma}\right\}}\] Scegliendo il minore dei due valori calcolati, si determina quanto è capace il processo sul lato peggiore, quello cioè rappresentato dalla coda della gaussiana più vicina al limite di tolleranza. Se Cpk è maggiore di 1, l’ampiezza 6s dei dati cade completamente nei Limiti di Tolleranza ; un Cpk compreso tra 0 e 1 indica che una parte dei prodotti del processo cadono oltre i Limiti, ed infine un Cpk negativo indica che la media dei dati non è nella specifica. Un Cpk uguale ad 1 indica che il 99,73% delle parti prodotte è nei limiti di tolleranza, cioè devono essere respinte solo 3 parti su 1000. Schematicamente il Cpk può essere interpretato nel seguente modo:
- \(Cpk > 1 \Rightarrow\) buon mezzo di lavorazione.
- \(Cpk = 1 \Rightarrow\) si è sul limite della lavorazione di pezzi non buoni;
- \(0 < Cpk < 1 \Rightarrow\) si lavorano dei pezzi non buoni;
- \(Cpk = 0 \Rightarrow\) la metà dei pezzi sono fuori tolleranza;
- \(-1 < Cpk < 0 \Rightarrow\) più del 50% dei pezzi sono fuori tolleranza;
- \(Cpk < -1 \Rightarrow\) la quasi totalità dei pezzi sono fuori tolleranza;
Molte aziende chiedono indici Cpk di 1,33 o 2 ai loro fornitori. Un indice di 1,33 significa che la differenza tra la media m e il Limite di Tolleranza è 4s (dato che 1,33 è 4/3). Con un Cpk di 1,33, il 99,994% del prodotto è nella specifica. Un miglioramento da 1,33 a 2 può essere giustificato in taluni casi per ottenere un numero maggiore di prodotti vicino al target ottimale, migliorando così le performance del prodotto, la sua vita, la soddisfazione del consumatore e riducendo i costi di garanzia e i problemi di assemblaggio. Non sempre però l’obiettivo è di avere indici Cpk sempre più alti per ogni processo, o parte di processo ; è invece preferibile effettuare prima un’analisi dei costi e dei benefici che comprenda anche il grado di soddisfazione del cliente, per determinare quali processi debbano essere migliorati e in che misura questo sia economicamente conveniente.
Relazione tra Cp e Cpk: in base alle relazioni viste, per un dato processo Cpk non può essere maggiore di Cp. Se la media è esattamente centrata sul punto medio della specifica, allora Cpk=Cp. Cp può quindi indicare quanto migliore sarebbe Cpk se il processo fosse realizzato in modo che il centro della distribuzione fosse il più vicino possibile al punto medio della specifica ; Cp, inoltre, specifica se la distribuzione degli individui, se centrata, può adeguarsi alle tolleranze imposte; Cpk, invece indica se le azioni di miglioramento del processo conducono in questa direzione.
DETTAGLIO DELLA NOSTRA CONSULENZA E DELLA NOSTRA FORMAZIONE
PER OGNI PROGETTO POTETE CHIEDERE UN FINANZIAMENTO!
Torna sopra

